|
The Twenty-First Century
by
Don Robertson
©
2005 Rising World Entertainment
Part
Five: The Spiral of Octaves
<-previous
The
Basics: Consonance
and Dissonance The
reality of consonance and dissonance is very important for an understanding of the effects of music. The traditional teachings about the
subject, however, were often tossed aside by writers,
musicologists, teachers, and composers during the twentieth century
in order to accommodate the
negative music that dominated so much of the century. It is time
now to bring
those teachings back. I believe that this is the most important
musical concept
that we will embrace in the 21st Century.
I
found that the music theory website Theory on the Web
has a very nice graphic
representation on the subject. Let's see what they have to say:
WHAT
"THEORY
ON THE WEB"
HAS TO SAY
If
we look at the interval of each note above the
fundamental (reducing those greater than an octave) we
discover that the perfect intervals of P8 [Perfect
Octave] and P5 [Perfect fifth] are closest to the fundamental. These most strongly
"fit" or reinforce the fundamental, forming
what we call a consonance.
As we move from left to right (farther away from the
fundamental) the frequencies are not as closely related,
and so we consider those intervals more dissonant.
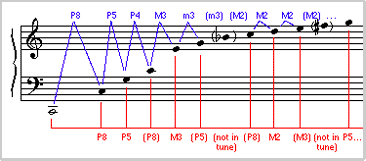 Also
important is the set of intervals between each of the
notes. Including the intervallic inversions, we may
derive a more comprehensive chart of relative consonance
and dissonance that has influenced musicians of all
periods. Since the tritone does not appear in the
series, it is the most removed or dissonant interval.
One may also think of consonance and dissonance in terms
of harmonic stability and instability, since this is how
composers have used these intervals in their music. 
Visit SMU's Theory on the Web
website at www.smu.edu/totw |
The
Octave as a Sine Wave
Georges
Gurdjieff, the important Russian spiritual teacher said that the
law of octaves was based upon the discontinuity of all
vibrations in nature, as they do not develop uniformly, but with
periodic accelerations and retardations. The original impulse
becomes alternately stronger and weaker. This could be a
phenomenon similar to the AC cycle. This cycle of alternating
electrical vibrations can be viewed by means of an oscilloscope
or with a computer program such as Sound
Forge. Called the duty cycle, it appears as such.
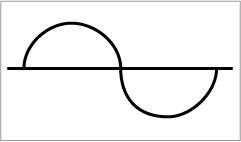
All
sounds are made up of these cycles. The cycles take place in the
time domain. By using a brilliant mathematical formula
known as the Fourier transform, these cycles can be translated
into the frequency domain, where we find that the timber of the
sound depends upon the strength of overtones, the higher
harmonics of the fundamental tone.
The
duty cycle can be equated to a circle broken at its diameter
with the bottom half twisted 180 degrees or to the continuous
movement of a spiral. Alternating current (AC) obeys the laws of
the duty cycle: energy alternates with no energy. Home
electricity in the United States alternates sixty times per
second, thus it is called 60 cycles, or 60 Hertz. An electric
light bulb does not continually burn, but flashes sixty times in
one second, faster than our eyes can follow, so we perceive the
appearance only of continuous light. This would not be the case
when light is powered by a battery, as batteries produce direct
current (DC).
Musical
tones can be represented using the mathematical symbols of
trigonometry, signs and cosigns, and the imaginary numbers of
calculus. Computer systems that generate musical tones, such as
synthesizers, do so using these mathematical formulas. All of
this is based on the alternation of the duty cycle.
I
have something new that I would like to present, something that to my knowledge
has not been proposed before: the octave as a
sign wave:

In the great
keyboard of nature, encompassing all phenomena, octaves
accumulate in
a giant spiral, each phenomena appearing in a different
frequency range, in different octaves. Matter vibrates at a
lower frequencies, sound occupies another region of this
"cosmic keyboard," color appears in another, higher,
octave, and so on. It is all vibratory: "maya," as it
is called in India. The phenomenon created by the vibrations in
any octave is always different, but the octave patterns
themselves are the same...the same law controls everything.
That is why Newlands called his original research "The Law
of Octaves."
The duty cycle of the sine wave has two phases: Phase I is the positive
phase of the duty cycle,
Phase II is the negative. Notice that there are two places where the cycle
touches "0" (the line): at the beginning of the duty
cycle ("C"), and as it crosses over the line from the
positive phase to the negative at F#, the interval that
cuts the octave into two sections, and as we see from the
"Theory on the Web" chart, the
most dissonant of intervals, called the tritone.
During
the twentieth-century, many composers, just as I did for several
years, made an icon out of
the tritone (also called the augmented forth or diminished fifth),
but in times past, this wasn't the case. From the 13th Century
to the 19th it was called diabolus in musica, or the devil in music,
and
composers were very careful of how they handled tritones in
their music. Taken by
themselves, the tritone creates a very disturbing sound. To my
knowledge, it was
probably only during the late 19th century that tritones were
first attempted in
a bare configuration by composers to
denote the presence of evil and suspense.
The cycle begins
on the left on moves to the right as it makes it's course moving away
from C towards Db, D, and E. To understand the consonance or
dissonance of the pitches, we implement two tone generators, one
maintaining a constant "C" pitch, the other increasing
in pitch as it follows the path of the duty cycle forward. The dissonance begins right away,
as the second tone generator moves up slightly from C on to Db,
the discordant minor 2nd interval, then it gradually decreases: the two pitches
grate against each other at first, but
the sound becomes less dissonant as
the interval of D (a major second) is reached, then Eb (the
minor third interval), then E (the major third interval). Finally
we arrive at the perfect interval of the forth. The cycle re-approaches
the line, and when it touches it,
we hear the tritone that splits the octave in half. Next we move
to the perfect
fifth. Even though F and G are as close to the line as Db and B, they
are perfect concords, unlike Db and B, both dissonant
intervals.
This is a very interesting situation.
Continuing the movement from the
perfect fifth concord, next we arrive at Ab (minor sixth), A
(major sixth) as dissonance increases to its maximum just before
touching the line at the octave, the most perfect consonance.
[Notice
that the three notes in the first half of the duty cycle are DEF
(The first three notes of a minor scale), and in the other half
GAB (the first three notes of a major scale).]
When you look at
a scale in this manner, some of the tuning ratios appear very
flexible.
For example, there is an
area around E that is at the top of the curve. E can be a little
sharp, a little flat...it is still the third. That is why there
are different thirds used in some scales of other cultures, ranging from the low third of
Darbari
Kanada in North Indian classical music, to the high third of
some middle-eastern music. The same goes for
sixths. The musicians in India know this, that is why they
identify variations of tone with shrutis, which are not a
22-note scale per say as some western musicians would have us
believe, but ways to account for slight variations of pitch. And
this is why the slight out-of-tuning condition of the
equal-tempered scale doesn't kill us (as some would have us
believe).
The
Enneagram
While
teaching in Russia during the first world war, Gurdjieff
described something about octaves that had not been publicly
known before. He stated that there were two places in the octave,
represented by the major scale, where retardation of the vibrations takes place. These places
are between the notes E and F and between the notes B and C.
These are the two places on the keyboard where there are no
sharp or flat note (black) keys between the white keys. Octaves,
according to Gurdjieff, develop according to whether or not
these places where retardation of vibrations take place are
“filled.” In the right development of these octaves, these
places are filled by the energy of octaves that run in parallel
to the given octave. This process of filling in Gurdjieff calls
a shock. Processes,
institutions, laws and other things all progress through time
according to the law of octaves, and therefore these two shocks
in the octave are a part of the development process.
Gurdjieff stated that if development continues without the
shocks being filled in, then the line of development constantly
changes.
The way he described it, if octaves – as a principal
of nature – develop unimpeded, the development looks as if it
is proceeding along a straight line, but every time one of the
two points in the octave is reached where a shock occurs, even
though development of the process that the octave represents
appears to be progressing forward along a straight line, the
development of the process actually jogs a little, causing what
would be compared to a jog in the line. The development
continues and after the progress through the series of octaves
has gone on for a particular amount of time, what was considered
to be development along a straight line has actually turned into
a development in the opposite direction! Further
continuation will bring the development back to the same
direction that it started in. This is actually a full duty
cycle, or one full revolution on a spiral.
The law
of octaves, with this intrinsic circular motion generating a
spiral, governs all activity and shows how organizations,
religions, and governments -- if allowed to develop without
conscious knowledge concerning the application of the ‘filling
in’ of these shocks -- always develop into something that is
opposite to what was originally intended.
The Octave with Two
Added Shocks
When asked why one shock correctly
appeared between the E and the F, but the other, instead of
appearing between B and C, appeared between G and A, Gurdjieff
stated that this demonstrated the nature of the shock that
occurred when passing from one octave to the next. He also said
that every completed whole, every organism, is an enneagram, but
that each of these enneagrams does not have an inner triangle
(3,6,9). 142857 is the working of the corporeal scheme, the
triangle is the presence of higher elements in the organism.
This inner triangle is possessed by plants, for example, from
which come our “drugs”: hemp, poppy, hops, tea, coffee,
tobacco.
Octaves and the Overtone Series
The cosmic keyboard is a repeating pattern of octaves each
vibrating at different, albeit proportional, frequencies. The overtone series is quite another thing.
Thus we
have a Pythagorean
comma.
The
sequence of octaves and the overtone series are two phenomenon that occur in nature. They are separate, but work together.
A
keyboard consists of octaves of pitches that range from low
to high. We could extend our piano's 88 keys to included
sub-sonic and super-sonic sounds, but that would be little use
if we could not hear the music that we created, but this does illustrate how
octaves are vibratory frequencies that extend in both directions
beyond the realm of sound.
The Overtone Series through Time
It
is very interesting to observe that over a period of hundreds of years, as
the understanding and use of harmony developed in Europe, higher
partials in the overtone series were gradually incorporated harmonically and melodically
into the music.
During
the time of early organum
around the 9th-10th centuries, harmonizing with parallel fifths and
fourths predominated. Later, the third and sixth was added,
yielding the first use of three-note polyphony in European
church music (C,E,G).
During the Renaissance period, the
fourth note, the seventh (C,E,G,Bb) was added, but
as a passing note. During the Baroque, it began to stand on its
own. Classic era composers began using other than the standard,
dominant, seventh chord, mostly as passing chords (not standing
alone) and the ninth chord began to come into use (C,E,G,Bb,D).
Romantic composers like Schubert and especially Franz
Liszt began using the ninth chord more boldly. Gabriel
Fauré used ninth-chord block harmonies in his famous
mid-1870s song Après
un Reve. Cesar
Franck introduced standalone ninth chords in his violin
sonata and in one of his last works, Ghiselle, a
beautiful opera that has unfortunately for music lovers remained unperformed for
the past century. Richard Wagner
eleventh (C,E,G,B,D,F#), and thirteenth (C,E,G,B,D,F#,A)
chords in his dramatic works, along other unusual harmonies,
and this opened the door to higher partials incorporated into melodic and
harmonic elements in music.
It was the 19th century French
composers, all of them studying Wagner and many of their
works unknown today, who began experimenting with music that
used higher-partial chords with the 11th and 13th more consistently. Debussy
and Scriabin
demonstrated the use of chords that employed
higher partials, and it was Scriabin who was able to demonstrate
the use of higher partials coordinated with the higher astral
planes in some of his later works such as his 8th and 10th piano
sonatas.
Later in the century, jazz musicians will begin using these
chords in their music, especially after Charlie Parker
studies Debussy's music and incorporates upper
partials in his saxophone solos.
The
overtone series
represents the laws of life itself, the inner dimension. The
repeating octaves are the occurrence on the outer planes, the
phenomena. The series outlines the octave and the laws of harmony that
govern creation.
| Alexander
Scriabin is a very important Russian composer, although
you won't find him in many English-language "Great
Composer Books" that go on and on about Prokofiev
and Shostokovich. Myself, I would trade all of those
composer's music for just one final listen to the first movement of Scriabin's Second Piano Sonata. His earlier music is ravishing, the
Preludes Opus 11, 15, 16, 31 and 33 for example, the Mazurkas
Opus 25, the first three symphonies and the piano
concerto. But if you want to see how he transcended and
advanced into the astral realms (as Corinne Heline
describes) listen to the 8th
Piano Sonata, and the 10th. No one had gone that far
before nor probably has since. Scriabin, however, not
only wrote very positive music, he also wrote very
negative. He was experimenting. He was an amazing
pianist, but refused to play his own Piano Sonata No. 6 because
it was so
dark! He named his 7th Piano Sonata the White Mass, and the
9th Piano Sonata, the Dark Mass. |
Tuning
A
heated subject is that of how scales should be tuned. That which
is known as just intonation is the scale
defined according to the overtone series, all the notes related to the scale base note (C) by rational numbers. This is nature at it's best,
all the intervals are perfectly in tune.
Pianos
today are tuned by a system
called equal
temperament, where
certain intervals were slightly detuned, making the tuning of
intervals in all the keys the
same. That's why a
modern piano can't be tuned 'by ear', unless the tuner has a
well trained ear and knows how many 'beats' (beats occur when
pitches are out-of-tune with each other) per second is needed
for the correct out-of-tuneness that is necessary for equal temperament. (I wrote a software system for my
Synclavier called "BACH". When you changed keys, the
just intonation changed with the modulation!).
This century will unfold many different
kinds of new music based on different tunings. Some of these
tunings will conform to natural principles such as the overtone
series and the golden mean and will prove to have a sympathetic
relationship to our sympathetic nervous systems and be
beneficial and healing, while others will not.
There
have been many temperaments that have come forth over the years, such as the
Pythagorean
scale, the mean-tone
scale, and the Werckmeister
scale. What will be important to all discussions of
tuning will be the work of researchers working with the science
of healing, through sound, and many discoveries will be
made in that area. What I propose is for my readers to take a
look at what is on the web:
Tuning on the Web
Barbara
Hero
An
Introduction to Historical Tuning
La
Monte Young's Well Tuned Piano
Just
Intonation Explained
Phi
Music
Jorgensen's
Tuning
Jorgensen's
Tuning: Amazon Link
Chrysalis
Foundation
Lucy Tuning
Ernest
McClain
PrimaSounds
Ray Tomes
The Last
Word
Music
in the 21st Century will be based on the overtone series and the
consonant intervals. In addition to new music, we will bring back
to our concert halls the great music we have neglected or
forgotten about from the past and the great spiritual traditions in
music used by the ancient civilizations of our planet that still
preserve their music. When healing returns to music, then
healing will be given back to the world, and healing will be
needed. As earthquakes, wars,
disasters, global warming and pandemics loam before us, we realize
more and more that we are creating the future. This is why the overtone series is
returning to music.
All
the great composers understood it: study the masterpieces.
"In
the great ancient cultures of India, China, and Greece, the
understanding of the transformational power of music and its
role in society was much more developed than it is today. The
master musicians of the Vedic civilization were also enlightened
masters or rishis whose consciousness was completely in tune
with all the laws of nature that govern the entire creation.
They truly exemplified the meaning of the Sanskrit aphorism
"Aham brahmasmi": I am the totality. Not only did they
intellectually understand the underlying musicality of the
structure of the cosmos, they lived and breathed it, and were
thereby able to cognize and produce music of a particularly
celestial nature."
From
Paul
Stokstad
Don Robertson
The year 2005...five years into the new century and moving
forward....
<-previous
|

